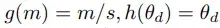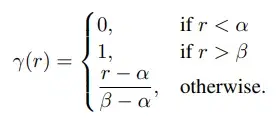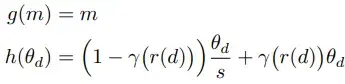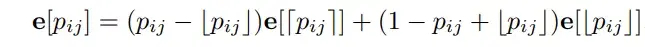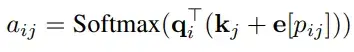Latest from Queryloop
Stay updated with our latest research findings, product developments, and insights into AI optimization
Research
Linear Rope vs NTK vs YaRN vs CoPE
Zain ul Abideen
July 13, 2024
17 min read
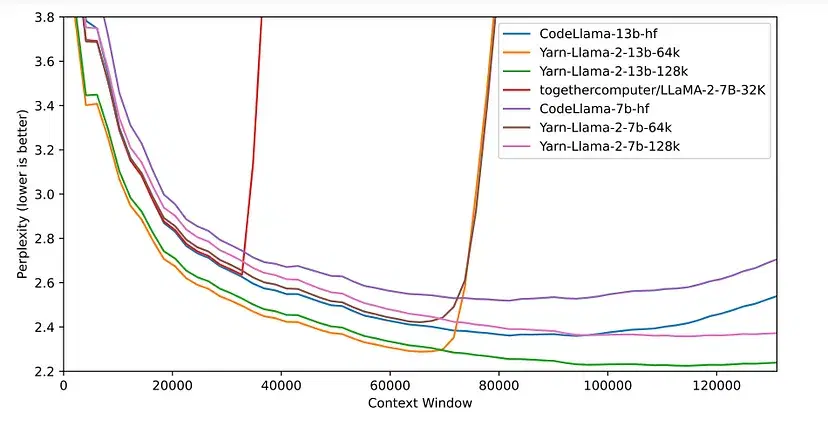
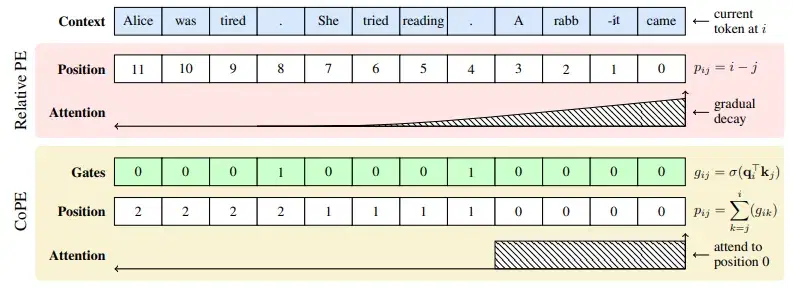
Comparison of various positional embeddings.
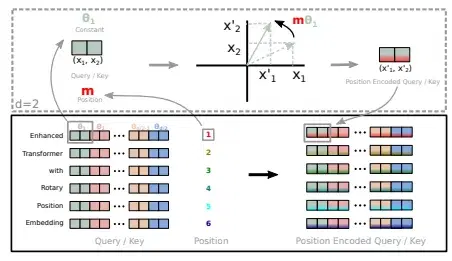
When processing sequences such as text, the ordering information is clearly critical. To incorporate ordering information and rather not treat sequences as sets, encoding position information is vital. Positional encoding achieves this by assigning an embedding vector to each position and adding that to the corresponding token representations. There have been many Positional Encoding techniques introduced: Absolute-PE counts tokens from the start of a sequence, Relative-PE counts backward starting at the current token. We will discuss some of the more advanced position encoding methods: RoPE and its variants (Linear, NTK, YaRN), CoPE.
Rotary Position Embedding (RoPE)
Rotary Position Embedding (RoPE) leverages the positional information into the training process of pre-trained models by encoding the absolute position with a rotation matrix and meanwhile incorporating the explicit relative position dependency in the self-attention formulation. The key idea is to encode relative position by multiplying the context representations with a rotation matrix. Also, RoPE decays with the relative distance increased.
The intuition behind RoPE is: to simply rotate the affine-transformed word embedding vector by the amount of angle multiples of its position index to incorporate the relative position embedding.
RoPE Implementation
Now let's implement the RoPE formulation:
RoPE Variants
Based on the rotation matrix/rotation angles and how they precompute the cos and sin frequencies, there are three variants of RoPE. Furthermore, to extend the model's context length beyond the pretrained limit, some method-dependent functions are introduced as discussed below.
Linear RoPE
In Linear, they modify the above RoPE equation by introducing the following method dependent functions g(m) and h(θ_d):
Neural Tangent Kernel (NTK)
NTK-aware interpolation resolves the problem of losing high-frequency information when interpolating the RoPE embeddings by scaling high frequencies less and low frequencies more, instead of scaling every dimension of RoPE equally by a factor s. This is done simply by performing a base change on the value of θ.
Yet Another RoPE Extension (YaRN)
YaRN introduces a ramp function which is further incorporated in method dependent functions.
Contextual Position Encoding (CoPE)
Contextual Position Encoding (CoPE) is context-dependent PE allowing positions to be conditioned on the context of previous tokens and incrementing position on only certain tokens (for example, period in a sentence), thus enabling counting of different levels of position abstractions such as words or sentences.
CoPE Implementation
Here's how the CoPE method works:
CoPE Gating Mechanism
Gating decides which tokens to include for counting positions using their context vectors and computes a gate value for every query-key pair. A gate value of 1 means the token is considered in the position counting, while a value of 0 means it is ignored.
CoPE - Computing Positions
To compute positions, the gate values between the current token and all tokens preceding it are added. Each position may represent a token/word/sentence number in the given sequence. To calculate limited positions i.e. if gates are sparsely activated (when counting sentences), we can cover the whole context of sequence length T with fewer positions and clamp each position within the maximum possible position. It's evident position values are float values since they add sigmoid outputs [0,1] and each ith-position value is a float within [0, i]. Thus the positions are not learnable and cannot be computed by an embedding layer.
CoPE - Interpolating Position Embeddings
To overcome the limitation of learning an embedding layer due to the floating position values, a learnable position embedding e[p] is assigned to each integer position in the sequence, then the positional embedding of the ij-th element will be a simple interpolation between two closest integer embeddings weighted by the fractional position values computed above. Finally, the attention can be computed by adding the position embeddings in the key vectors.
Implementing CoPE
To save memory and compute, q.e[p] matrices are precomputed for further interpolation and then finally added into the context. The CoPE class can compute the interpolated values as follows:
CoPE in Attention Class
The CoPE embeddings are added to the context as follows:
attn_mtx += self.cope(q, attn_mtx) is where CoPE embeddings are added to the context.
My rough notes regarding implementation details of YaRN:
LlmNLPMachine LearningDeep Learning